経緯
前回、CNNモデルのパラメータ・計算量削減手法の一つであるpointwise convolution(pw畳み込み)について解説した。
pw畳み込みはHW方向の次元を削減し計算量とパラメータを減らすものだったが、それの対極をなすものとして、レイヤー方向の次元を削減するdw畳み込みがあるので、簡単に説明する。
mobilenet等はpw畳み込みと、dw畳み込みの繰り返しであり、この二つの概念が理解できれば、モデルの中身が理解できるはず。
概要

dw畳み込みの基本的な構成部品は上図の通り、nxnx1の畳み込みフィルタである。基本的には、これを入力層のHxWx1のレイヤに適応し、HxWx1の出力を得ている。
ここで留意すべき点は、畳み込みフィルタ(nxnx1)、入力層(HxWx1)、出力層(HxWx1)共に、層方向の次元が1であること。
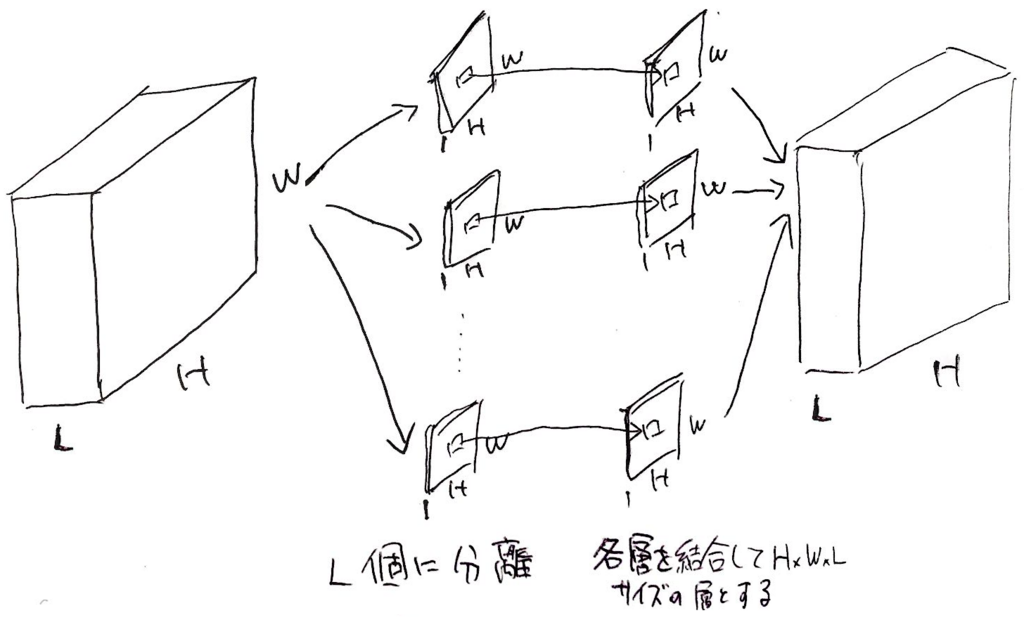
それでは、入力のレイヤー数が増えた場合はどうなるのか?入力層がHxWxLとなった場合の処理を上図に示す。
先に説明した構成要素である、畳み込みフィルタ(nxnx1)、入力層(HxWx1)、出力層(HxWx1)の次元数を守るために、入力層を一旦1次元のレイヤに分離をし、HxWx1の畳み込みを加えたのち、再び層を結合することで、入力層(HxWxL)、出力層(HxWxL)の次元を確保している。
通常のnxnxLの畳み込みはフィルターが全て層にかかっていることに比べると、計算量が大幅に削減できていることが一目でわかる。
ただし、dw畳み込みでは、各層ごとに畳み込みをするため、層間の関係性は全く考慮されないため注意が必要。通常はこれを解決するためにpw畳み込みとセットで使うことが多い。
#実際の実装ではこの様な処理をしているわけではないが、計算的には等価。一般的な説明とも少し違う説明の仕方だけれど、概念的にはこの理解の方法が一番理解しやすいのでは?
depthwise convolutionのパラメータ数、計算量
dw畳み込みのパラメータ数と計算量についても定量的に示しておく。基本的に、dw畳み込みではレイヤー数は不変なので、入力層のレイヤ数L=出力層のレイヤ数Lとなる。
・パラメータ数はnxnxL、通常のnxn畳み込みのパラメータ数はnxnxLxLであることから、パラメータ数は1/Lで済む。
・計算量も同様にnxnの畳み込みに比べて1/Lとなる。
depthwise convolutionのメリット
最大のメリットは、やはり計算量の削減ができること。特にCPUでは(GPUに比べて)nxnの畳み込みは時間がかかるので、dw畳み込みで畳み込み計算量を減らすことで、大幅に速度を改善できる。